In der Mathematik stoßen wir oft auf Zahlen, die außerhalb unserer Alltagsvorstellungen liegen. Eine besonders ungewöhnliche Zahl ist die imaginäre Zahl i, definiert als die Quadratwurzel von -1. Diese Zahl erscheint zunächst widersprüchlich, denn keine reelle Zahl, quadriert, ergibt ein negatives Ergebnis. Doch gerade hier setzt die Mathematik auf ihre Kreativität: Durch die Einführung imaginärer Zahlen wird es möglich, Quadratwurzeln negativer Zahlen zu berechnen und Lösungen für Gleichungen zu finden, die bisher keine reelle Lösung hatten.
Die Zahl i und das System der komplexen Zahlen, zu dem sie gehört, eröffnen nicht nur neue Lösungswege in der Algebra, sondern finden auch in vielen Wissenschaftsbereichen wie Physik und Elektrotechnik Anwendung. Dieser Artikel erklärt die Bedeutung und die Eigenschaften der imaginären Einheit, beleuchtet die mathematische Herleitung und zeigt, warum i unverzichtbar für die moderne Mathematik ist.
Und ja, es gibt noch weitere besondere Zahlen in der Mathematik. Aber keine Panik! Wir erklären jede einzelne Schritt für Schritt.
Grundlagen der Zahlentheorie
Um die imaginäre Zahl i und ihre Bedeutung zu verstehen, lohnt sich ein Überblick über die verschiedenen Zahlmengen in der Mathematik. Die natürlichen Zahlen (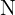
), wie 0, 1, 2 usw., bilden den Grundstock, auf dem das Zählen und die Arithmetik basieren. Die ganzen Zahlen (
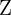) erweitern diese Menge, indem sie auch negative Zahlen einschließen. Rationale Zahlen (
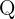) gehen noch einen Schritt weiter und umfassen alle Brüche, also Zahlen, die als Verhältnis zweier ganzer Zahlen dargestellt werden können.
Doch nicht alle Zahlen lassen sich als Brüche ausdrücken. Reelle Zahlen (
) erweitern die rationalen Zahlen und beinhalten auch irrationale Zahlen wie π oder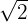 
, deren Dezimaldarstellung nicht endet oder sich wiederholt.
Nun kommen wir zu den komplexen Zahlen (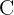
), die eine neue Ebene der Mathematik eröffnen. Sie setzen sich zusammen aus einem Realteil und einem Imaginärteil und haben die Form a + bi, wobei a und b reelle Zahlen sind und i die imaginäre Einheit darstellt. i ist definiert als die Quadratwurzel von -1, also 
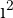= -1.
Diese Definition löst das Problem, dass negative Quadratwurzeln in den reellen Zahlen keine Lösung haben. Die Einführung der komplexen Zahlen ermöglicht es, mathematische Konzepte und Anwendungen in Naturwissenschaften und Technik zu erweitern, die in den reellen Zahlen allein nicht möglich wären.
Natürliche Zahlen (N):
Alle positiven ganzen Zahlen, die zum Zählen verwendet werden (meistens ab 1 oder 0: z. B. 1, 2, 3, …).
Ganze Zahlen (Z):
Alle natürlichen Zahlen sowie ihre negativen Gegenstücke und die Null (z. B. -2, -1, 0, 1, 2, …).
Rationale Zahlen (Q):
Alle Zahlen, die als Bruch aus zwei ganzen Zahlen dargestellt werden können, wobei der Nenner nicht null ist. (z. B. 
Reele Zahlen (R):
Alle rationalen und irrationalen Zahlen. Dazu gehören Zahlen mit nicht periodischen, unendlichen Dezimalstellen, wie π oder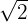
Komplexe Zahlen (C):
Zahlen, die sowohl einen reellen als auch einen imaginären Teil enthalten, dargestellt als a + bi, wobei i der imaginäre Teil ist.
Schon mal gehört, dass es sogar eine goldene Zahl gibt??Was diese genau meint, erfährst Du ebenfalls bei uns.
Die Zahl i: Eigenschaften und Definition
Das i wird in der Mathematik als eine komplexe Zahl definiert, deren Anwendung eigentlich einfach ist, aber die eine gewisse Fähigkeit zur Abstraktion erfordert.
Die Zahl i ist für viele Gymnasialschüler oft ein erstes, unerwartetes Treffen mit abstrakten Konzepten in der Mathematik. Sie wird als imaginäre Einheit bezeichnet und ist der Schlüssel, um mit negativen Quadratwurzeln zu arbeiten.
Warum brauchen wir die imaginäre Einheit?
Bestimmte mathematische Gleichungen – speziell quadratische Gleichungen – haben in der Menge der reellen Zahlen keine Lösung, da es keine reelle Zahl gibt, deren Quadrat negativ ist. Zum Beispiel ergibt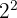 
= 4 und auch 
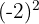= 4. Das Produkt zweier negativer Zahlen ist immer positiv. Daher hat keine reelle Zahl ein Quadrat, das eine negative Zahl ergibt.
Doch was passiert, wenn wir trotzdem versuchen, eine Quadratwurzel aus einer negativen Zahl zu ziehen? Diese Herausforderung führte zur Definition der imaginären Einheit i, die als i=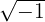
definiert ist und als besondere Eigenschaft 
= -1 besitzt.
Die Form komplexer Zahlen
Komplexe Zahlen stellen eine Erweiterung der reellen Zahlen dar und haben die allgemeine Form a + bi, wobei a der Realteil und bi der Imaginärteil ist. Hier sind sowohl a als auch b reele Zahlen und i steht für die imaginäre Einheit.
Ein Beispiel:
Die Quadratwurzel von -4 ergibt 2i, da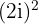 
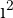= 4 = -4.
Jede Zahl der Form bi wobei b eine reele Zahl ist und ungleich 0, wird als reine imaginäre Zahl bezeichnet.
Du brauchst dringend Mathe Nachhilfe? Wir von Superprof finden den perfekten Lehrer für dich- in deiner Stadt (z.B. Mathe Nachhilfe Wien).
Mach dir keine Sorgen wegen deiner Schwierigkeiten mit der Mathematik. Ich kann dir versichern, dass meine noch größer sind.
Albert Einstein
Die Bedeutung von i: Ein neues Zahlenkonzept
Da 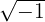in den reellen Zahlen keine Lösung hat, ist i eine Art mathematisches Hilfskonzept, das uns ermöglicht, Quadratwurzeln negativer Zahlen zu konzipieren. Mit i lässt sich eine ganze Familie neuer Zahlen schaffen, die sogenannten imaginären Zahlen.
Hast du dich eigentlich schonmal gefragt, was perfekte Zahlen sind?
Die Geschichte der Zahl i
Die komplexen Zahlen tauchen im 16. Jahrhundert auf, als der italienische Mathematiker Gerolamo Cardano (1501 –1576) sie einführte, um eine Gleichung dritten Grades zu lösen.
Raphael Bombelli (1526-1572 oder 1573) ist der erste Mathematiker, der Berechnungsregeln für "unmögliche Zahlen" in der Algebra ausgearbeitet hat, bei denen die ersten Eigenschaften komplexer Zahlen auftreten.
Die Zahl i entstand aus der Suche nach nicht reellen Lösungen für Gleichungen dritten Grades, Polynomgleichungen mit einer Kubikwurzel.
1637 taufte der französische Philosoph René Descartes (1595-1650) diese unmöglichen Werte "imaginäre Zahlen".
Später erscheint die Bezeichnung i im Jahr 1777 nach dem Vorbild von Leonhard Euler (1707-1783) - ja, genau: Der Erfinder der Zahl e zur Berechnung der Exponentialfunktion - für die Zahlen, die er als "unmöglich" oder als "imaginär" einstuft.
Im 19. Jahrhundert werden diese komplexen, rein imaginären Zahlen, insbesondere dank der Werke von C. F. Gauss (1777-1855), als eigenständige Zahlen betrachtet.
Der Zweck von komplexen Zahlen wie e oder i, ist laut dem französischen Mathematiker Augustin Louis Cauchy (1789-1857), "in verkürzter Form Ergebnisse darzustellen, die ziemlich komplex erscheinen", mit "einer Kombination von algebraischen Zeichen, die für sich selbst nichts bedeuten".
Da sie algebraische Berechnungen erleichtern, werden komplexe Zahlen auch in geometrischen Berechnungen eingeführt.
Du brauchst Statistik Nachhilfe? Entdecke das Angebot von Superprof und finde deinen perfekt auf dich zugeschnittenen Kurs.
Warum verwenden wir reine imaginäre Zahlen?
Die Verwendung und Anwendung komplexer Zahlen ist vielfältig, auch wenn sie einem überflüssig erscheinen, wenn man für die Abiturprüfung paukt...
Warum gibt es also imaginäre Zahlen und wofür braucht man sie?
Die Zahl i macht es möglich, Gleichungen zu lösen, die keine echte Lösung haben.
In der Mathematik ist es ein No-Go, zu akzeptieren, dass eine Gleichung keine Lösung hat! Wo es Zahlen gibt, gibt es auch eine Lösung!
Hier sind zwei Beispiele:
- Die Gleichung x + 8 = 1 hat keine Lösung in der Menge der natürlichen Zahlen 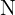(weil die natürlichen Zahlen nur positive ganze Zahlen ab 1 umfassen). Die Lösung x=−7 gehört jedoch zur Menge der ganzen Zahlen (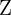)=, da sie negativ ist.
- Die Gleichung x² = 2 (x = 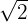) hat keine Lösung in der Menge der rationalen Zahlen, aber eine in der Menge der irrationalen Zahlen, da es keine rationale Zahl gibt, deren Quadrat genau 2 ergibt. Die Lösung x = 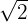gehört zur Menge der irrationalen Zahlen, weil 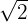keine endliche oder periodische Dezimaldarstellung hat und daher irrational ist.
Dank der imaginären Zahl ist es möglich, absolut alle Gleichungen zu lösen.
Die Verwendung der imaginären Zahl hat auch in der physikalischen Forschung und in der Elektrizität für Fortschritte gesorgt: Die Zahl i hat das Studium von gedruckten Schaltungen von Computern ermöglicht und ist daher die Grundlage der Computerrevolution des 20. Jahrhunderts!
Rechnen mit der imaginären Zahl i
Um die Rechenoperationen mit komplexen Zahlen zu verstehen, nehmen wir eine einfache Formel der Form a + bi, wobei a und b reelle Zahlen sind und i die imaginäre Einheit (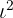
= -1) darstellt. Schauen wir uns an, wie Addition, Subtraktion, Multiplikation und Division von komplexen Zahlen durchgeführt werden.
Addition und Subtraktion
Um zwei komplexe Zahlen zu addieren oder zu subtrahieren, addiert oder subtrahiert man die Realteile und die Imaginärteile separat:
(2 + 3i) + (4 + 5i) = (2 + 4) + (3 + 5)i = 6 + 8i
Multiplikation
Bei der Multiplikation zweier komplexer Zahlen verwenden wir die Regel 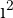= -1:
(2 + 3i) x (4 + 5i) = 2 x 4 + 2 x 5i + 3i x 4 + 3i x 5i = 8 + 10i + 12i + 15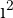
Da 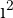= -1, vereinfacht sich der Ausdruck zu:
8 + 22i - 15 = -7 + 22i
Division
Die Division komplexer Zahlen ist etwas aufwändiger. Dazu multiplizieren wir Zähler und Nenner mit dem „konjugierten Wert“ des Nenners. Das Konjugat einer Zahl a + bi ist a - bi.
Beispiel: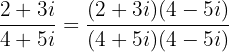 
Der Nenner wird vereinfacht mit 
+ 
= 16 + 25 = 41. Für den Zähler ergibt sich:
8 - 10i + 12i - 15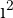 = 23 + 2i
Der Endergebnis ist also:
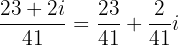
Diese Rechenoperationen zeigen die Basis für die Arbeit mit komplexen Zahlen. Um sicher im Umgang damit zu werden, ist Übung hilfreich. Probiere es selbst auf Papier, um die Logik hinter den Schritten zu verstehen.
Erfahre alles über die Zahl null.
Wie lernt man imaginäre Zahlen?
Es stimmt, dass Online-Ressourcen sehr hilfreich sein können, um die komplexen Zahlen zu entdecken und zu verstehen.
Bücher sind jedoch ebenfalls eine große Hilfe für Deine mathematischen Erkenntnisse! Nichts ist besser als ein Buch mit Erklärungen und Übungen zu komplexen Zahlen oder mathematischen Formeln.
Hier sind einige Beispiele für Nachschlagewerke zu komplexen und imaginären Zahlen:
- Klaus Fritzsche: Mathematik für Einsteiger
- Yvonne Story, Rainer Schwenker: Mathematik kompakt
- Wolfgang Walter: Analysis 1
- Gernot Stroh: Algebra
- Uwe Storch, Hartmut Wiese: Lehrbuch der Mathematik. Band 1
- Frank Kretzschmar: Komplexe Zahlen für Dummies
- Uwe Storch, Hartmut Wiese: Grundkonzepte der Mathematik
Diese Werke richten sich an Studenten, Anfänger der Mathematik sowie Liebhaber komplexer Zahlen. Sie bieten eine allgemeine Einführung in komplexe Zahlen sowie konkrete Fallstudien mit imaginären Zahlen.
Wenn man sie einmal wirklich verstanden hat, sind komplexe Zahlen gar nicht mehr so komplex! Und dank der vielen Ressourcen, findest Du sicher etwas Passendes für Dein Niveau und Deine Ziele.
Wenn Du eine Auffrischung Deiner Kenntnisse vor einer Prüfung benötigst - ob es sich nun um Primzahlen, Geometrie oder Alegbra handelt - ist es ratsam, die Ressourcen zu multiplizieren - arbeite sowohl mit Büchern als auch online und mit Lehrern!
Dir gefällt unser Artikel? Hinterlasse eine Bewertung!
Loading...
